

a) Investigating Fibonacci numbers:
Here we choose m from Natural numbers include 0, and define f as a function f(m) = f(m-2) + f(m-1). We are assuming f(0) = 1 and f(1) = 1.
For example: if we choose m=2 then f(2)= f(2-2) + f(2-1) = f(0) + f(1) = 1 + 1 = 2
We call Fibonacci numbers to the sequence of f(m) values.
As you can see from table when the values of m increase then the values of f(m) increase rapidly and the ratio of m / f(m) getting smaller.
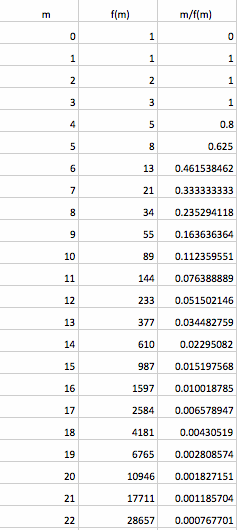
Here is a graph for Fibonacci numbers. When the value of m increases then the value of f(m) increases. As you see after m = 15 and bigger values, the value of f(m) increases rapidly.
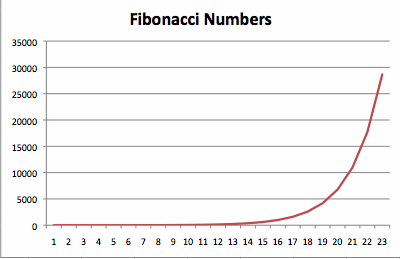
If we continue to give big values for m then limit of ratio m/ f(m) converges to zero.Here is a graph of m / f(m)
Here is a spreadsheet for Fibonacci Numbers:
Fibonacci Numbers and Golden Ratio:
Now let look at Fibonacci numbers and its relation with Golden ratio. When the value of f(m) increased the ratio of f(m+1) / f(m) converges to 1.618..... In mathematics this value called Golden Ratio. You can see that in the below table:
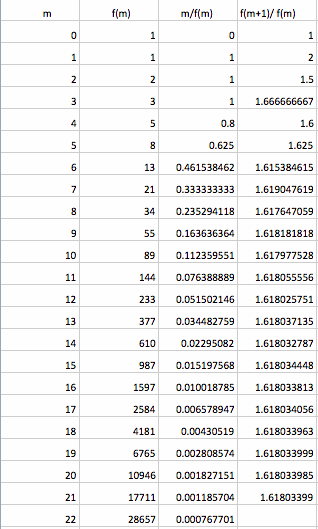
A spreadsheet for Golden Ratio:
b) Lucas Sequence:
Now, what happens if we take f(0) = 0 but f(1) = 3 instead of 1? Here is a spread sheet which shows the new values of f(m)'s:
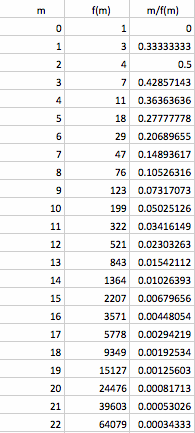
This new sequence called Lucas Sequence in math. Here is a graph for Lucas Sequence:
As you see below graph the ratio of m / f(m) converges 0 as n---> infinity.
Here is a spreadsheet for this sequence: